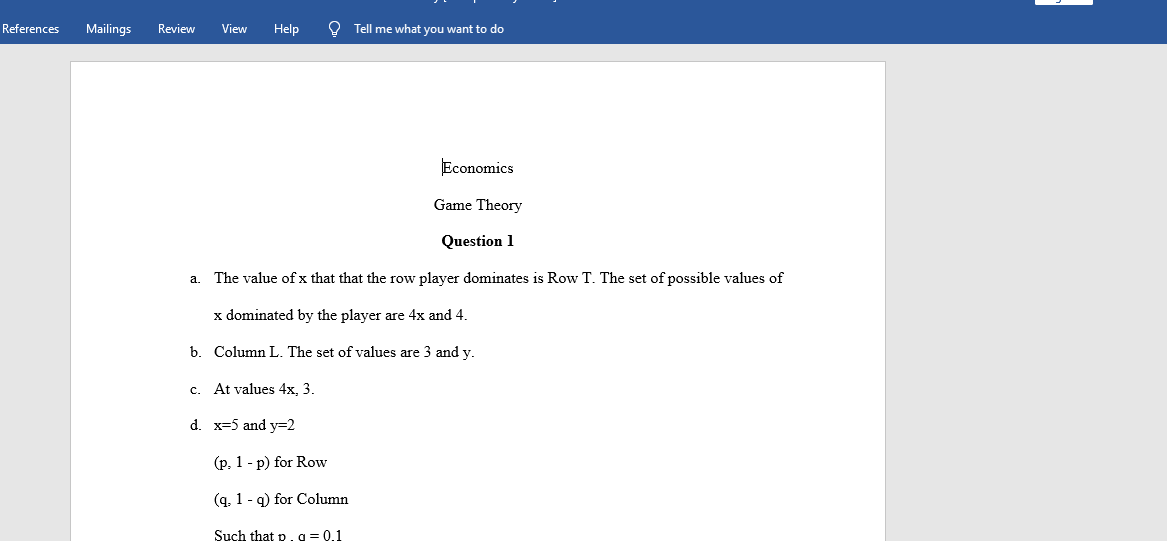
Consider the following strategic-form game G1px, yq where x, y P R are parameters of the game.
Q1 [25pts]
Consider the following strategic-form game G1px, yq where x, y P R are parameters of the game.
Figure 1: Strategic-form game G1px, yq
Row:
Column:
L R
T 4x, 3 4, 2
B 2, y x, 7
1. For what values of x does the Row player have a strictly dominated strategy? Provide both the set of possible values of x and the strategy that is dominated.
2. For what values of y does the Column player have a weakly dominated strategy? Provide both the values of y and the strategy that is dominated.
3. For values of px, yq is pB,Rq a pure strategy Nash Equilibrium. For what values of px, yq is pT,Lq a pure strategy Nash Equilibrium?
4. Now assume that x “ 5 and y “ 2. Find a totally mixed Nash Equilibrium, (i.e., pp, 1 ́ pq for Row, pq, 1 ́ qq for Column, such that p, q P p0, 1q.)
Q2 [25pts]
Two firms are price-competing as in the standard Bertrand model. Each faces the market demand function Dppq “ 100 ́ p. Firm 1 has constant marginal cost c1 “ 40, while firm 2 has the constant marginal cost c2 “ 50. If either of the firms has the lower price, it captures the entire market, and when they charge exactly the same price, they split the
market evenly, as in the standard model.
1. Draw the profit function ⇡1pp1, p2q when p2 “ 60. (Mark sure to label all points of interest on all graphs: maximum values, axis crossings, points of discontinuity, axes labels)
2. Draw the profit function ⇡2pp1, p2q when p1 “ 60.
3. Write out the best-response correspondences B1pp2q and B2pp1q as functions of p2 and p1 respectively.
4. Is there an equilibrium for this game as defined?
5. Suppose S1 “ S2 “ t0.00, 0.01, 0.02,…, 1000.00u. That is, instead of any real number we force prices in whole cents.
(a) Why must there now be an equilibrium, regardless of the exact profit functions?
(b) Provide a Nash Equilibria in pure strategies for this game.
(c) Calculate the profits for each firm under any one of these equilibria, accurate to the nearest cent.
Q3 [25pts]
Recall in class, that we showed that the general solution for the N firm Cournot model was for each firm to produce pa ́cq
N . Now we will investigate more closely the three firm case. Each firm i P t1, 2, 3u simultaneously chooses a quantity to produce qi. The market price
is determined by an inverse demand which depends on the total quantity produced by all three firms Q “ q1 ` q2 ` q3, where the price per unit is given by PpQq “ max ta ́ Q, 0u. Each firm has the same marginal cost c of producing every unit of the good, such that a ° c ° 0. So the total profit is given by:
⇡i pq1, q2, q3q “
$
&
%
pa ́ q1 ́ q2 ́ q3q ̈ qi ́ c ̈ qi if q1 ` q2 ` q3 § a
́c ̈ qi if q1 ` q2 ` q3 ° a
1. Write out the best-response correspondence B1pq2, q3q for every possible combination of q2 and q3
2. Show that the symmetric Nash Equilibrium quantity for each firm is given by q‹
1 “
q‹
2 “ q‹
3 “ pa ́cq
4 . (I.e., show that this is a mutual best response)
3. Give an expression for each firm’s equilibrium profits ⇡ipq‹
1, q‹
2, q‹
3q as a function of a
and c at this equilibrium.
4. Provide any symmetric point ˆq1 “ qˆ2 “ qˆ3 such that each firm’s profit ⇡ipqˆ1, qˆ2, qˆ3q °
⇡ipq‹
1, q‹
2, q‹
3q.
Q4 [25pts]
Consider the following game. There are two players. Player 1 has 10 dollars, and proposes
any split of the ten dollars between himself and player 2 (i.e., A1 “ r0, 10s). Then, after
the proposal, player 2 can accept of reject the split. The payo↵s given by (a = accept, r =
reject)
u1px, aq “ 10 ́ x u1px, rq “ 0
u2px, aq “ x u2px, rq “ 0
1. How many subgames are there in this game? Describe the set of all subgames.
2. Verify that the following strategies constitute a Nash Equilibrium: p6; a if x • 6, r if x †
6q.
3. Consider another NE strategy profile that achieves the same outcome (i.e., x “ 6 and
accept).
4. In a subgame perfect NE, what must P2’s action be for any x ° 0?
5. Show that in a subgame perfect NE, P2 cannot reject (with any positive probability)
even after x “ 0. (Hint: assume this was the case and find a contradiction).
6. What is the unique subgame perfect NE of this game?
Answer preview for consider the following strategic-form game G1px, yq where x, y P R are parameters of the game.
Access the full answer containing 705 words by clicking the below purchase button